

A decision tree is a mechanical way to make a decision by dividing the inputs into smaller decisions. Like other models, it involves mathematics. But it’s not very complicated mathematics. We look at a graphic that will illustrate making a decision on whether to play golf based on the combination of temperature, humidity, the wind, and whether it is sunny, mild, not humid, and not windy then the decision to play golf is "yes".
A rule of thumb in logistic regression, if the probability is > 50% then the decision is true. So in this case, the determination is made that the child has chickenpox.
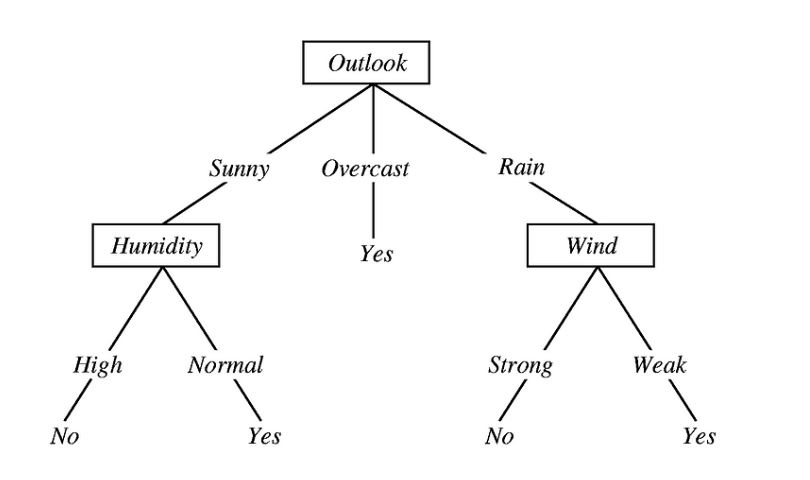
The tree is divided into decision nodes and leaves. The leaves are the decisions: yes or no. The nodes are the factors: windy, sunny, etc.
To see how a decision tree predicts a response, follow the decisions in the tree from the root (beginning) node down to a leaf node which contains the response. Classification trees give responses that are nominal, such as true or false. Regression trees give numeric responses.
Decision trees are relatively easy to follow; you can see a full representation of the path taken from root to leaf. This is especially useful if you need to share the results with people interested in how a conclusion was reached. They are also relatively quick.
The main disadvantage of decision trees is that they tend to overfit, but there are ensemble methods to counteract this.
Entropy
Entropy is the measure of purity (disorder). A high level of entropy means a high level of disorder (meaning low level of purity). Entropy is measured between 0 and 1.(Depending on the number of classes in your dataset, entropy can be greater than 1 but it means the same thing , a very high level of disorder.
This looks at the frequency distribution of decisions and then calculates a logarithm. For example, the complete matrix of factors that leads to the decision to play golf is fed into a table.
When entropy is zero then all the answers are the same. The process repeats itself, by dividing each decision into sub-conditions for each decision until entropy is zero. So the next step in the golf example is to look at the decision to play golf when it is sunny. Then look at the decision when it is sunny and windy. And so forth.
Sources