Bias-Variance Tradeoff

Bias and Variance are prediction errors when it comes to accuracy in any machine learning algorithm. Bias refers to how well your model can represent all possible outcomes, whereas variance refers to how sensitive your predictions are to changes in the model’s parameters. 

Bias and variance are two important properties of machine learning models. 

Bias

1. This is the difference between the prediction of the values by the ML model and the correct value. 
2. Being high in biasing gives a large error in training as well as testing data.
3. Its recommended that an algorithm should always be low biased to avoid the problem of Underfitting of Data.

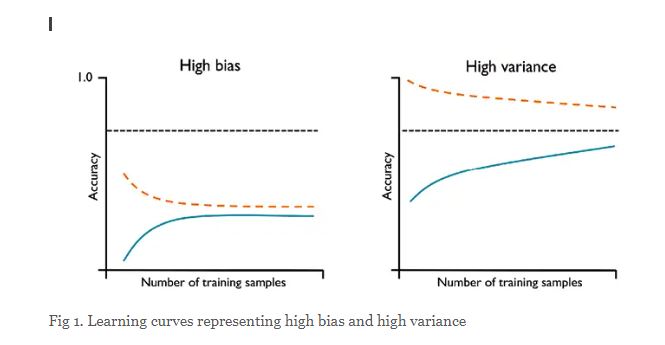
High Bias Models (Underfitting): The plot on the left side represents the model having both low training and validation accuracy. This indicates that that the model under fits the training data and thus, is the case of high bias. You may notice that as the training samples size increases, the training accuracy decreases and validation accuracy increases. However, the validation accuracy is far from the desired accuracy.

One way to tackle the high bias of machine learning models is to add more features to the training data. This will allow the model to learn more complex relationships and hopefully reduce the bias. Adding more features to a machine learning model can help reduce the model bias. This is because more features give the model more data to learn from, which can help it to become more accurate.

Another way to tackle high bias is to use a different machine learning algorithm that is better suited for the data. Finally, it is also possible to combine multiple models to create a more accurate prediction.

Variance

1. This is the variability of model prediction for a given data point and it tells us the spread of our data
2. The model with high variance has a very complex fit to the training data and thus is not able to fit accurately on the data which it hasn’t seen before
3. As a result, models with high variance perform very well on training data but has high error rates on test data
4. When a model is high on variance, it is then said to as Overfitting of Data. 
5. Overfitting is fitting the training set accurately via complex curve and high order hypothesis but is not the solution as the error with unseen data is high.
6. While training a data model variance should be kept low.

The plot on the right side represents a model that has large gap between training and validation accuracy. The training accuracy is larger than the validation accuracy. These models suffer from high variance (overfitting). You may notice that as the training samples size increases, the training accuracy decreases and validation accuracy increases. However, the training accuracy is much greater than validation accuracy and also desired accuracy.

Some of the ways to address this problem of overfitting are following:

• Add more data: Collect more training data; This may not always help, though as adding more data may result in noise.
• Remove less important features: Reduce the complexity of the model by removing noisy features; For unregularized models, you can use feature selection or feature extraction techniques to decrease the number of features
• Use cross-validation: Cross-validation is a technique that involves splitting your data into multiple sets, and then training your model on one set of data and testing it on another set of data. This helps to ensure that your model is not overfit to the data that it was trained on.
• Use regularization: This technique adds a penalty to the cost function of the model in order to discourage overfitting. This penalty can be added in different ways, such as by adding a constant to the cost function or by adding a term to the cost function that is proportional to the number of parameters in the model.

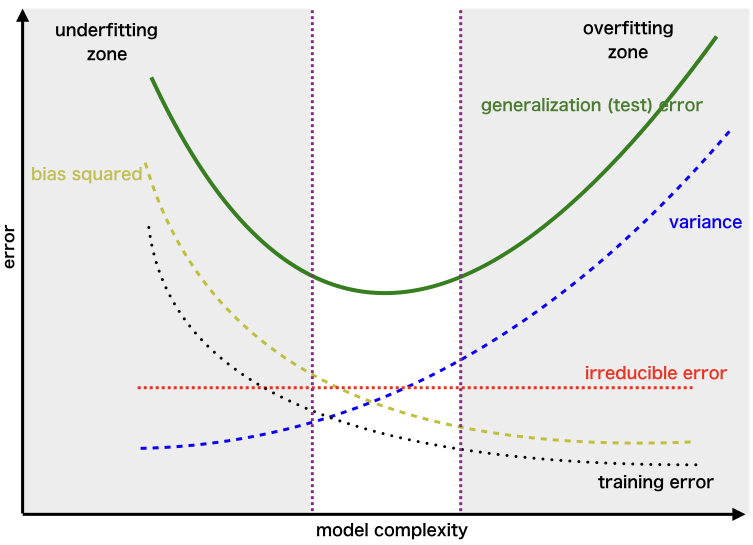
Bias-Variance Tradeoff

If the algorithm is too simple (hypothesis with linear eq.) then it may be on high bias and low variance condition and thus is error-prone. If algorithms fit too complex ( hypothesis with high degree eq.) then it may be on high variance and low bias. In the latter condition, the new entries will not perform well. Well, there is something between both of these conditions, known as Trade-off or Bias Variance Trade-off.

Sources

1. Vital Flux
2. Geeks4Geeks