Why LR is considered a linear model
While logistic regression is considered a linear model because of the linear relationship between the input variables and the log-odds of the output variable. It is not a linear algorithm in the sense that it does not use a linear equation o predict the output variable. Instead, it uses the logistic function to transform the linear combination of the input variables into a probability.
Variable Relationship
Logistic Regression is considered a linear model because the relationship between the input variables and the output variables is linear. In other words, the model is based on the assumption that the log-odds of the output variable is a linear combination of the input variables. Logistic regression is considered a generalized linear model because the outcome always depends on the sum of the inputs and parameters. Or in other words, the output cannot depend on the product (or quotient, etc.) of its parameters!
Logistic Relationship
It is important to note that while the relationship between the input and output variables is linear, the relationship between the output variable and the input variables is not linear, it is logistic. While logistic regression is considered a linear model because of the linear relationship between the input variables and the log-odds of the output variable, it is not a linear algorithm in the sense that it does not use a linear equation to predict the output variable. Instead, it uses the logistic function to transform the linear combination of the input variables into a probability.
Logistic Function
The logistic function, also known as the sigmoid function, is used to model the relationship between the input variables and the probability of the output variable being 1. The logistic function has an S-Shaped curve, which means that as the values of the input variables change, the probability of the output variable being 1 also changes in a non-linear way. The logistic function maps any real-valued number to a value between 0 and 1, which makes it suitable for modeling probabilities.
Objective
The objective function is to minimize the logistic function which looks like the image below:
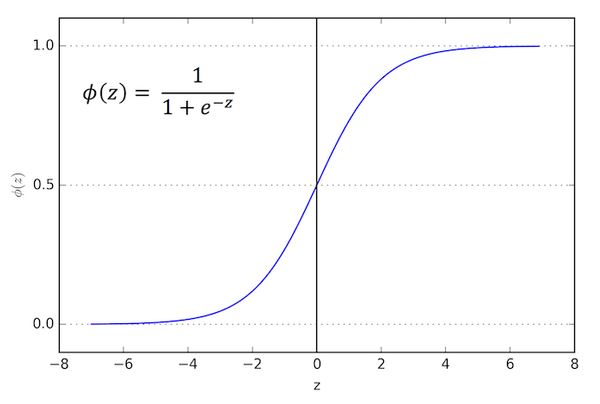
Now if the sigmoid function is larger than 0.5 (if z is larger than zero), the classification is of class 1. Although logistic regression produces a linear decision surface, the activation function doesn't look very linear at all.
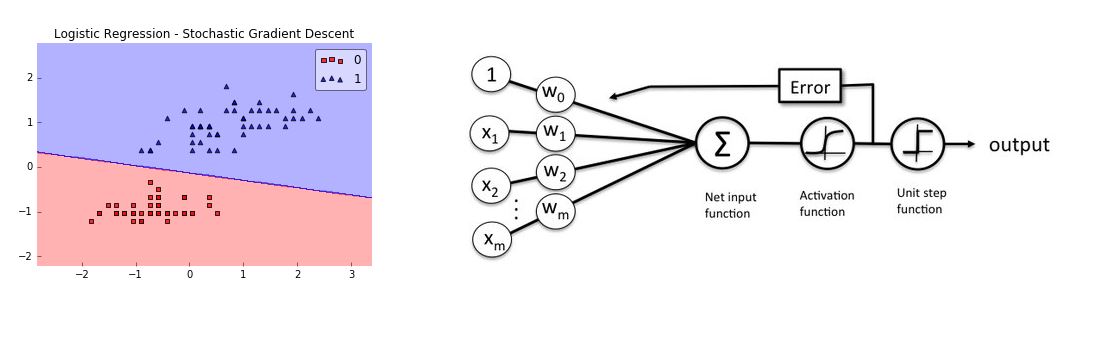
The net input function is simply the dot product of our input features and the respective model coefficients w:
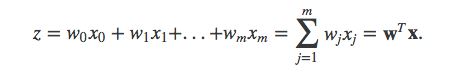
Assuming we have a sample training point x of 4 features (e.g. sepal width, sepal length, petal width, petal length in the Iris Dataset)
x = [1, 2, 3, 4]
Assuming the weight vector looks like this:
w = [0.5, 0.5, 0.5, 0.5]
When we compute the sigmoid function
z = w^T x = 10.5 + 20.5 + 30.5 + 40.5 = 5
thus
the reason why logistic regression produces a linear decision boundary is the additivity of the terms: Our outcome z depends on the additivity of the parameters, e.g., :
z = w_1 * x_1 + w_2 * x_2
There's no interaction between the parameter weights, nothing like w_1*x_1 * w_2* x_2 or so, which would make our model non-linear!
Practical Notebooks
- Students enrolling for any AI related course from Carnegie Training Institute have access to jupyter notebook, class exercises illustrating this reasoning.
Sources
