

It is based on the concept of dependent probability. If you roll a dice, the probability of getting a 6 is 1/6 since there are 6 sides. What is the probability that you get a 5 after rolling a 6? It’s not any different than if you rolled a 3 or any other number instead of a 5 as those are completely independent events. So the probability of rolling a 6 and then a 5 is (1/6)*(1/6).
Naive Bayes is a high-bias/low-variance classifier, which has advantages over logistic regression and nearest neighbor algorithms when working with a limited amount of data available to train a model.
Naive Bayes is also a good choice when CPU and memory resources are a limiting factor. Because naive Bayes is very simple, it doesn’t tend to overfit data and can be trained very quickly. It also does well with continuous new data used to update the classifier.
Naive Bayes is often the first algorithm scientists try when working with text (think spam filters and sentiment analysis). It’s a good idea to try this algorithm before ruling it out.
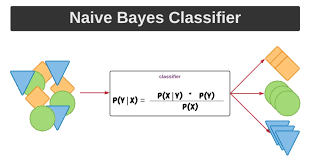
So if we want to answer the question: “what is the probability that a newly received email is spam given that it contains the word ‘lottery’?” That is calculated ((probability of spam given “lottery”) * (probability of spam for all mail)) / (probability of an email containing the word “lottery”).
Sources